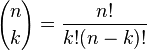Binomial coefficient C#

Ce que l’on appelle un Coefficient binomial en deux façons, un symbole de la Newton ?

Parfois, une situation o? nous avons besoin de déterminer le nombre de combinaisons des éléments de la collection. Il s’agit d’une situation que, contrairement aux apparences, il arrive tr?s souvent, mais pas toujours, il est nécessaire de faire des calculs, et les décisions sont prises de mani?re intuitive.

Par exemple, vous pouvez envisager plusieurs situations o? le choix est fait :

-A publié une série de 4 cartes ? collectionner des athl?tes cél?bres, et nous pouvons nous permettre que 2 d’entre eux. Avec ce jeu que vous pouvez choisir les numéros de la carte {1,2}, {1,3}, {1,4}, {2, 3}, {2,4}, {3,4}, et donc nous pouvons faire des choix différents 6.

-Favourite game numéro tire 5 numéros non répétitif de 60 disponibles. Le nombre de combinaisons est beaucoup plus grand que dans l’exemple précédent et imprimer tout cela prendrait beaucoup de place dans cet article.

-L’entreprise emploie 100 personnes, et la moitié d’entre eux recevront plus tôt ce mois-ci. Combien de combinaisons d’employés peuvent vérifier ici se pour produire ? Beaucoup d’employeurs refl?te pas sur cette question et faire votre propre ventilation.

La définition du Coefficient Binomial

Que se passe-t-il si, toutefois, nous aimerions savoir combien nous vraiment choix et quels sont-ils ? Puis, avec la formule définie par Newton, appelé coefficient Binomial ou binomial. Il s’agit d’une fonction de deux arguments qui sont des entiers. La solution est symbole de Newton, le nombre de combinaisons possibles de votre choix peuvent ?tre obtenus en sélectionnant les éléments de k dans un ensemble de n éléments ensemble. La définition du mod?le est comme suit :

Le résultat du symbole de Newton dans le code

Le code présenté représente la solution ? la formule ci-dessus, sans l’utilisation de la récursivité pour les forts. Il est appliqué dans la relation qui est créée au moment du compteur de pi?ces avec plus de raccourcissement du produit du dénominateur. Des précisions sur un exemple particulier devraient dissiper les doutes. Compteur en symbole de Newton va toujours ?tre plus grande que le dénominateur. Sélection de n = 8 et k = 5, vous obtenez une fraction :

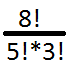Réduire le compteur (8!) avec un facteur plus élevé du dénominateur (5!), nous obtenons :

-au numérateur 6 * 7 * 8 (car 1 * 2 * 3 * 4 * 5 sera raccourcie),

-? utiliser dans le dénominateur de 1 * 3 ! (donc 1 * 2 * 3).

Dans le code suivant, le numéro 1 est multiplié par un autre valeurs de compteur (6 * 7 * 8) et divisé par les éléments suivants du dénominateur (1 * 2 * 3). Cette relation simplifie l’entrée et le code de travail pour une condition et une boucle.

long WyliczIloscGrup (n, k long de long) //zwraca le nombre de combinaisons
{
    Si (k > n-k)
        k = n-k ;
    long liczGrupy = 1 ;
    pour (int i = 0; i + k; et < +)
    {
        liczGrupy = liczGrupy * (n-i) ;
        liczGrupy = liczGrupy / (i + 1) ;
    }
    Return liczGrupy ;
}

Combinaisons de code de groupe

Parfois, informations sur le nombre de combinaisons possibles ne sont pas suffisantes et nous aimerions savoir quels sont les éléments qu’ils représentent. Le code est relativement simple dans le cas o? c’est le nombre d’éléments qui a tirer et combien est disponible. La situation se complique lorsque la fonction est censée pour ?tre universelle et utile pour toutes les valeurs.

Voici le code pour la fonction qui obtient la déj? présenté les param?tres n et k et retourne un tableau de tableaux. Retourne un tableau d’un tableau typé stocké dans chaque ligne avec les valeurs d’appartenance au groupe. Les lignes, donc vous pouvez interpréter comme juste un autre du groupe et de leurs colonnes est dessiné en eux.

L’algorithme doit ?tre éclairci, mais les grenouilles mieux comprennent il s’ensuit également l’exemple de n = 6, k = 4.

Définir les valeurs dessinés se fait dans le tout en boucle. Son premier appel stocke groupe initialement défini (1, 2, 3,…, k-dans notre exemple 1, 2, 3, 4). Les appels suivants ? la boucle augmente le dernier élément dans le tableau d’origine, jusqu’? la valeur maximale égale ? n l?-dessus (c.-?-d.-> 1, 2, 3, 5-> 1, 2, 3, 6). Lorsque cette valeur, la variable est décrémentée de 1, ce qui crée une référence ? un élément avec un indice inférieur (? ce stade, c’est la valeur de la position 3 égal ? 3, qui passe ? 4). Éléments avec des indices plus d’elle sont incrémentés de 1 ? l’égard d’une nouvelle variable (1,2 restent inchangés, 4 modifié il y a un instant et les éléments suivants 4 + 1 = 5, qui donne un autre groupe de 1, 2, 4, 5), et la variable p est encore une valeur de k pour que la référence au dernier élément.

Faisant référence ? des éléments avec des indices plus et plus petits s’effectue lorsque le dernier élément prend la valeur maximale de plus d’une fois, pour les éléments consécutifs (par exemple. pour la premi?re fois pour un groupe de 1, 2, 4, 6, o? p est réduit ? 3, la deuxi?me fois 1, 2, 5, 6, o? p est réduite ? 2). Le dernier groupe de réduire la variable ? 0 et Merci et nous compteur que c’est la derni?re des combinaisons possibles.

Détermination des groupes de k-tuples ? partir d'un ensemble de n éléments
int [] [] WyznaczGrupy (int n, int k)
{
    int i = 0, p = 0, count = 0 ;
    le nombre de groupes possibles de numéros-nombre de lignes dans le tableau
    long iloscGrup = WyliczIloscGrup (n, k) ;
    Déclaration de tableau k-aire pour différents groupes
    int [] pojedynczaGrupa = new int[k] ;
    la déclaration d'un tableau de tableaux pour tous les groupes
    int [] [] wszystkieGrupy = new int [iloscGrup][] ;
    pour chaque ligne est assigné un tableau vide est unidimensionnel, k-elementowa
    pour (i = 0; i iloscGrup ; j'ai ++ <)
        wszystkieGrupy[i] = new int[k] ;
    pour compléter le tableau de valeurs k-aire de 1 ? k
    pour (i = 1; i = i + k; < +)
        pojedynczaGrupa[i - 1] = i ;

    et enfin, moins nombreux que nous avons disponible (n)
    Si (k < n)
        p = k ;
    tous les n-temps doit ?tre établi
    instruction Else
        p = 1 ;

    Count-nombre de l'actuel groupe augmenté
    Tandis que (compteur < iloscGrup)
    {
        Lorsque le dernier élément du groupe est égal ? la valeur la plus récente disponible-> du dernier cas
        Si (pojedynczaGrupa[k - 1] == n)
            p est la position du tableau k-aire initialement définie ? laquelle le saut 
            pour augmenter sa valeur par l'un et selon elle, placez les éléments suivants.
            p-;
        instruction Else
            p = k ;

        Si (p &gt; 0) dépasse la portée des groupes définis, et (comte! = 0) ce n'est pas le premier groupe
        Si ((p > 0) && (comte! = 0))
        {
            pour (i = k; et > = p; i--)
                pojedynczaGrup[i - 1]a = pojedynczaGr[p - 1]upa +-p + 1 ;
        }

        la cession a créé un groupe unique ? la ligne correspondante dans l'ensemble de tous les groupes
        pour (int j = 0; j < k; j ++) //completion le rang suivant
            wszystkieGrupy[licznik][j] = pojedynczaGrupa[j] ;

            compteur ++ ;
    }
    Return wszystkieGrupy ;
}

Afficher toutes les combinaisons

Le code suivant a été introduit dans le collecteur d’une chaîne de données variables sur la composition des groupes et leur numérotation d’une mani?re agréable ? le ?il humain :

1-1 2 3 4 5
2-1 2 3 4 6
3-1 2 3 4 7
4-1 2 3 4 8
….

    Vue
    courbe int = 0 ;
    Count = 0 ;
    Tandis que (compteur < iloscGrup)
    {
        ligne ++ ;
        wyswietlwszystkieGrupy += ? n ? ;
        wyswietlwszystkieGrupy += ligne. ToString () ;
        wyswietlwszystkieGrupy += "" ;

        pour (int j = 0; j < k; j ++) //completion le rang suivant
            wyswietlwszystkieGrupy + = wszystki[licznik][j]eGrupy () + "" ;
        compteur ++ ;
    }