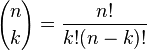Koeffizienten-Binomial-Binomialkoeffizient #

Was heißt ein Binomialkoeffizient in zwei Möglichkeiten-ein Symbol für das Newton?

Manchmal eine Situation, wo wir die Anzahl der Kombinationen der Elemente der Auflistung ermitteln müssen. Dies ist eine Situation, dass entgegen Auftritte, es sehr oft passiert, aber nicht immer, besteht die Notwendigkeit, Berechnungen anzustellen und intuitiv Entscheidungen.

Beispielsweise können Sie mehrere Situationen berücksichtigen, wo Wahl getroffen:

-Eine Reihe von 4 sammelbare Karten von berühmten Sportlern veröffentlicht, und wir können davon nur 2 leisten. Mit diesem Set können Sie wählen, die Karte Zahlen {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, und so können wir 6 verschiedene Möglichkeiten machen.

-Anzahl Lieblingsspiel zeichnet 5 nicht wiederholenden Zahlen ab 60 zur Verfügung. Die Anzahl der Kombinationen ist viel größer als in dem vorherigen Beispiel und alles dauert viel Platz in diesem Artikel drucken.

-Die 100 Mitarbeiter sind beschäftigt, und die Hälfte von ihnen erhalten Anfang des Monats. Wie viele Kombinationen der Mitarbeiter können hier auftreten? Viele Arbeitgeber nicht reflektiert dies und eigene Aufschlüsselung zu tun.

Die Definition der Binomialkoeffizient

Was ist, wenn jedoch möchten wir herausfinden wieviel wir wirklich Wahl und was sie sind? Dann mit der Formel von Newton definiert, Binomial oder binomialen Koeffizienten genannt. Dies ist eine Funktion von zwei Argumente, die nicht negative ganze Zahlen sind. Die Lösung ist Newtons Symbol wie viele Kombinationsmöglichkeiten Ihrer Wahl durch Auswahl der k Elemente aus einer Menge von n-Elementsatz abgerufen werden können. Die Definition des Modells lautet wie folgt:

Das Ergebnis des Newtons-Symbols im code

Der Code stellt die Lösung dar, um die obige Formel, ohne die Verwendung von Rekursion für die starken. Sie gilt in der Beziehung, die zum Zeitpunkt der Verkürzung Teile Zähler mit mehr das Produkt der Nenner erstellt wird. Ein besonderes Beispiel Klärung sollten Zweifel zu zerstreuen. Zähler in Newtons Symbol wird immer größer als der Nenner ist. Auswählen von n = 8 und k = 5 erhalten Sie einen Bruchteil:

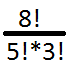Verringerung des Zählers (8!) mit einem höheren Faktor des Nenners (5!), erhalten wir:

-im Zaehler 6 * 7 * 8 (weil 1 * 2 * 3 * 4 * 5 verkürzt werden wird),

-zur Verwendung in den Nenner von 1 * 3! (also 1 * 2 * 3).

Im folgenden Code ist die Nummer 1 multipliziert mit einem anderen Indikatorwerte (6 * 7 * 8) und dividiert durch die folgenden Elemente des Nenners (1 * 2 * 3). Diese Beziehung vereinfacht die Eingabe und funktionierenden Code für eine Bedingung und eine Schleife.

lange WyliczIloscGrup (lange n, lange k) //zwraca die Anzahl der Kombinationen
{
    Wenn (k > n-k)
        k = n-k;
    lange LiczGrupy = 1;
    für (Int i = 0; i + k; und < +)
    {
        LiczGrupy = LiczGrupy * (n-i);
        LiczGrupy = LiczGrupy / (i + 1);
    }
    Rückkehr LiczGrupy;
}

Gruppe-Codevarianten

Manchmal Informationen über die Anzahl der möglichen Kombinationen ist nicht ausreichend, und wir möchten herausfinden, welche Gegenstände sie bilden. Der Code ist relativ einfach in der Fall, wenn es ist, die Anzahl der Elemente, die gezeichnet werden und wieviel zur Verfügung steht. Die Situation wird noch komplizierter, wenn die Funktion universell und für alle Werte nützlich sein soll.

Die folgenden ist der Code für die Funktion, die die zuvor vorgestellten Ruft die Parameter n und k, und gibt ein Array von Arrays. Gibt ein Array von typisiertes Array gespeichert in jeder Zeile mit den Werten der Zugehörigkeit zu der Gruppe. Die Zeilen, so dass Sie es, wie gerade interpretieren können eine andere von der Gruppe und deren Spalten wie in ihnen gezeichnet.

Der Algorithmus erfordert Klärung, aber Frösche besser zu verstehen, folgt auch das Beispiel für n = 6, k = 4.

Definieren der gezeichneten Werte erfolgt in der While Schleife. Ihre ersten Aufruf speichert ursprünglich definierte Gruppe (1, 2, 3,…, k-in unserem Beispiel 1, 2, 3, 4). Nachfolgende Aufrufe der Schleife erhöht das letzte Element in das ursprüngliche Array bis zum Maximalwert drauf gleich n (d.h.-> 1, 2, 3, 5-> 1, 2, 3, 6). Wenn dieser Wert ist die Variable um 1, wodurch einen Verweis auf ein Element mit einem niedrigeren Index verringert (zum jetzigen Zeitpunkt ist es der Wert der 3 Position gleich 3, die auf 4 geändert wird). Elemente mit größeren Indizes daraus werden um 1 hinsichtlich einer neuen Variablen erhöht (1,2 bleiben unverändert, 4 geändert, vorhin und nachfolgende Elemente 4 + 1 = 5, wodurch eine weitere Gruppe von 1, 2, 4, 5), und die Variable p ist wieder ein k-Wert so, dass der Verweis auf das letzte Element.

Verweisen auf Elemente mit mehr und kleineren Indizes durchgeführt wird, wenn das letzte Element den maximalen Wert mehr als einmal für aufeinander folgende Elemente (zB übernimmt. zum ersten Mal für eine Gruppe von 1, 2, 4, 6, wo p auf 3, das zweite Mal 1 reduziert ist, 2, 5, 6, wo p ist auf 2 reduziert). Die letzte Gruppe der reduzieren die Variable auf 0 und Dank und wir Marke, dass dies der letzte der möglichen Kombinationen ist.

Bestimmung der Gruppen von k-Tupel aus einer Menge von n Elementen
Int [] [] WyznaczGrupy (Int n, Int k)
{
    Int i = 0, p = 0, Anzahl = 0;
    die Anzahl der möglichen Gruppen von Zahlen, die Anzahl der Zeilen im array
    lange IloscGrup = WyliczIloscGrup (n, k);
    k-äre Array-Deklaration für einzelne Gruppen
    Int [] PojedynczaGrupa = new In[k]t;
    die Deklaration eines Arrays von Arrays für alle Gruppen
    Int [] [] WszystkieGrupy = new Int[iloscGrup] [];
    für jede Zeile zugewiesen ist, wird ein leeres Array eindimensional, k-Elementowa
    für (i = 0; i IloscGrup; ich ++ <)
        WszystkieGrupy[i] = neue In[k]t;
    Das Array von k-äre Werte von 1 bis k ergänzen
    für (ich = 1; i = i + k; < +)
        PojedynczaGrupa[i - 1] = i;

    und schließlich weniger zahlen als wir haben verfügbar (n)
    Wenn (k < n)
        p = k;
    Alle n-Count wird erstellt
    Else-Anweisung
        p = 1;

    Count-die Nummer der aktuellen erweiterte Gruppe
    Während (Zähler < IloscGrup)
    {
        Wenn das letzte Element in der Gruppe gleich den neuesten verfügbaren Wert->'s's letzter Fall
        Wenn (PojedynczaGrup[k - 1]a == n)
            p ist die Position des k-äre ursprünglich definierten Arrays, denen der Sprung 
            um den Wert um eins und danach zu erhöhen, legen Sie die folgenden Elemente.
            p-;
        Else-Anweisung
            p = k;

        Übersteigt (p > 0) die definierten Gruppen und (Graf! = 0) Dies ist nicht die erste Gruppe
        Wenn ((p > 0) && (Graf! = 0))
        {
            für (ich = k; und > = p; i--)
                PojedynczaGru[i - 1]pa = PojedynczaGr[p - 1]upa + p + 1;
        }

        die Zuordnung erstellt eine einzelne Gruppe auf die entsprechende Zeile in der Menge aller Gruppen
        für (Int j = 0; j < k; j ++) //completion nächste Zeile
            WszystkieGrupy[licznik][j] = PojedynczaGrupa[j];

            Zähler ++;
    }
    Rückkehr WszystkieGrupy;
}

Alle Kombinationen anzeigen

Der folgende Code wurde eingeführt im Kollektor eine Zeichenfolge variabler Daten über die Zusammensetzung der Gruppen und ihre Nummerierung in einer Weise, die angenehm für das menschliche Auge:

1-1 2 3 4 5
2: 1 2 3 4 6
3: 1 2 3 4 7
4: 1 2 3 4 8
….

    Anzeigen
    Int-Linie = 0;
    Count = 0;
    Während (Zähler < IloscGrup)
    {
        Linie ++;
        WyswietlwszystkieGrupy += "n";
        WyswietlwszystkieGrupy += Linie. ToString ();
        WyswietlwszystkieGrupy += "";

        für (Int j = 0; j < k; j ++) //completion nächste Zeile
            WyswietlwszystkieGrupy + = Wszystk[licznik][j]ieGrupy () + "";
        Zähler ++;
    }